MLP Funktionsweise
 Graphische Darstellung der Funktionsweise von MLP-Netzwerken am Beispiel zweier Funktionen f(x) und f(x1,x2)

Zu approximierende Funktion : (1)

MLP :
(2)
Wobei ist.
Darstellung des MLP Netzausganges, wobei jeweils ein Hidden Neuron bei der Berechnung nicht berücksichtigt wurde. Bei MLP(ohne h1) wurde z.B. der Term in Formel (2) nicht berücksichtigt. Darstellung der Hidden–Neuronen. In Bereichen in der die Hidden-Neuronen (Flächen) waagrecht verlaufen, leisten sie nur einen konstanten Beitrag zur Ausgabe. Die Form der Ausgabefunktion kann in diesen Bereichen nicht mit modlliert werden. Man erkennt, das Hiddenneuronen nur in bestimmten Bereichen Einfluß auf die Ausgabe haben, da ein Hiddenneuron ein S-förmige Funktion ist, die an beiden Enden waagrecht verläuft. Sie kann daher nur im Biegungsbereich masgeblich zur Ausgabefunktion beitragen. Mann erkennt auch, das eine stark gekrümmte zu approximierende Funktion sehr viele hidden Neuronen benötigt um alle Windungen der Funktion nachzubilden.


Bei zwei Input-Variablen () entsprechen die S-förmigen Kurven (tanh sigmoid usw.) S-förmige Flächen Jedes Hidden-Neuron entspricht einer Fläche. Alle Hidden-neuronen in Linearkombination bilden die Netz-Ausgabe. Beispiel einer solchen S-förmigen Fläche:
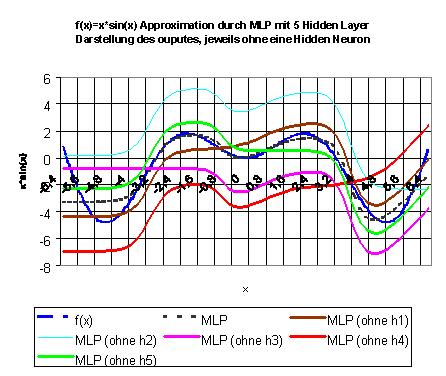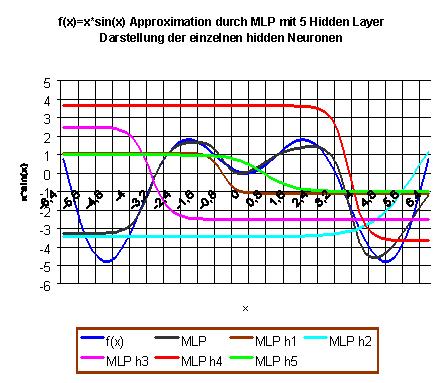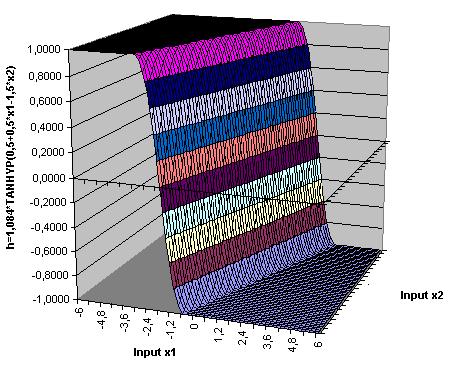Aktivierungsfunktion eines Hidden-Neurons für zwei Inputvariable h(x1,x2)=1,084*tanh(0.5+0.5*x1-1,5*x2)

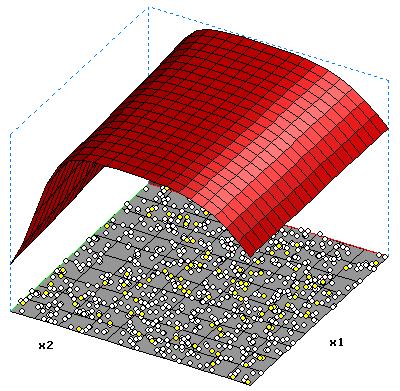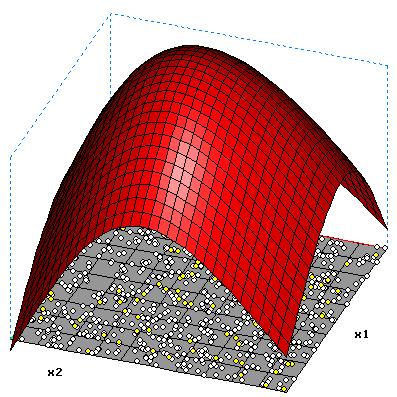
Um beispielsweise einen Zylinder zu approximieren werden mehrere solcher Flächen kreisförmig angeordnet. (Daten: 1000 Datensätze x1,x2 zufällig aus [0,1], Output ist 1 wenn sonst 0.
Bespiel für zwei, drei, vier und zehn Hidden-Neuronen (Flächen)
2 Hidden-Neuronen o= 0.046-0.870*tanh(-0.896+1.131*x1-0.247*x2)-0.967*tanh(-0.127-1.546*x1+0.363*x2)
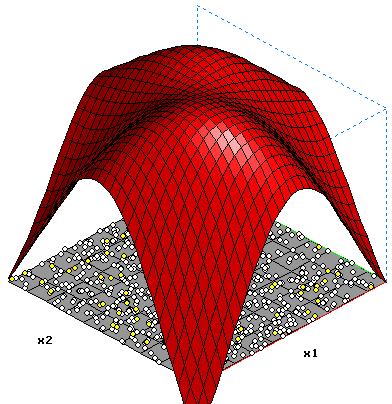
3 Hidden-Neuronen o= -2.081-1.446*tanh(-0.254-2.585*x1+0.497*x2)-1.244*tanh(-0.013+0.188*x1-2.654*x2)-1.713*tanh(-1.646+1.015*x1+0.855*x2)
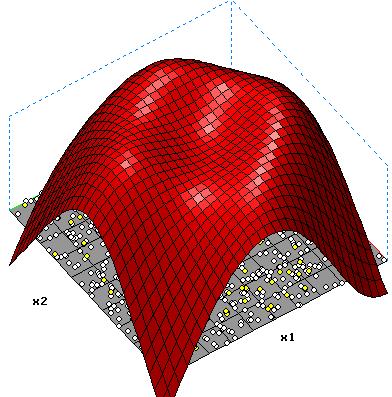
4 Hidden-Neuronen o= 1.578-1.718*tanh(-0.783-0.153*x1+1.159*x2) -1.702*tanh(-0.864-1.256*x1+0.101*x2)+1.321*tanh(2.061- 1.289*x1+1.378*x2) +1.371*tanh(-0.792-1.427*x1+1.354*x2)
10 Hidden-Neuronen

Approximation anhand von Datenpunkten am Beispiel der XOR-Funktion

Xor ist eine Binäre Funktion (exklusives oder) die nicht linear seperabel ist und deshalb nicht von einem Singel-Layer-Perceptron erlernt werden kann.
Wertetabelle:

X1

X2

xor

0

0

0

0

1

1

1

0

1

1

1

0

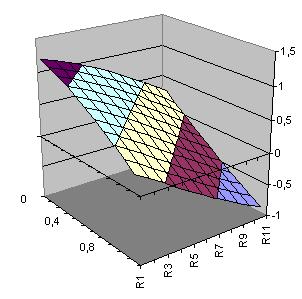
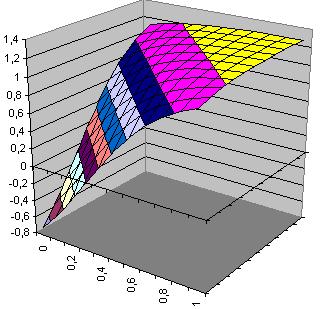
Netztopologie: Zwei Eingangsneuronen (x1,x2), zwei Hidden-Neuronen und ein Ausgabeneuron
Fläche Hidden-Neuron 1
h1(x1,x2)=-1.684*tanh(-0.917+0.759*x1+0.754*x2) 		Fläche Hidden-Neuron 2
h2(x1,x2)= -1.368*tanh(0.621-1.985*x1-1.957*x2)


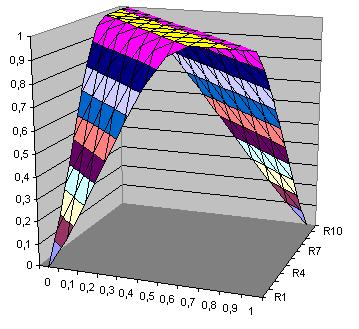
Ausgabe des MLPs als Linearkombination der Hidden-Neuronen Flächen

Xor(x1,x2)= -0.465+h1(x1,x2)+ h2(x1,x2)

Xor(x1,x2)= -0.465-1.684*tanh(-0.917+0.759*x1+0.754*x2) -1.368*tanh(0.621-1.985*x1-1.957*x2)


XOR mit einem Hidden-Neuron und Direktverbindungen

Verwendet man nur ein Hidden-Neuron und Direktverbindungen von jedem Eingang zu jedem Ausgang, so wird die Ausgabe als Linearkombination einer Ebene und einer S-förmigen Fläche (Hidden-Neuron-Fläche) erzeugt.

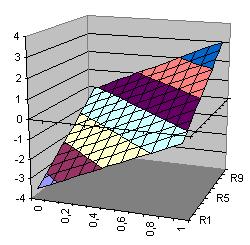
Ebene Direktverbindungen
Ebene(x1,x2)= 3.345+3.369*x1+3.093*x2
 		Fläche Hidden-Neuron
h1(x1,x2)=-3.453*tanh(2.053+1.765*x1+1.675*x2)
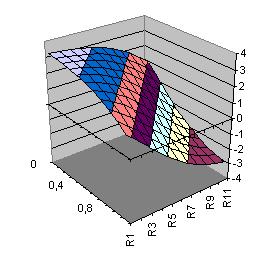
 		Ausgabefunktion Xor
Xor(x1,x2)= 3.345-3.453*tanh(-2.053+1.765*x1+1.675*x2) +3.369*x1+3.093*x2


Zur Startseite